Order Of Subgroup Divides Order Of Group

Order Of Subgroup Divides Order Of Group - Since the con-jugates of N are also. Elements have order 1424.

Group Theory The Center Of A Group G Is A Subgroup Of G Proof Group Theory Maths Exam Theories

Subgroups Definition Order of a Group.

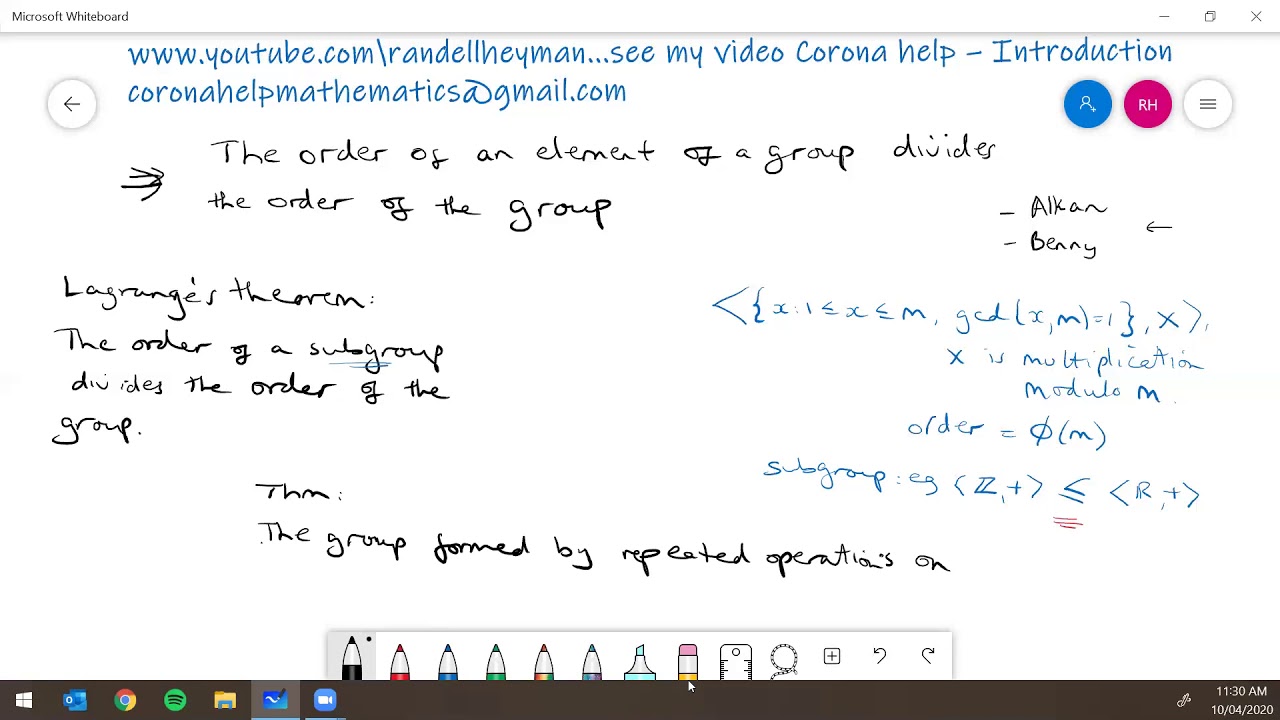
Order of subgroup divides order of group. If H is a subgroup of G then ordG ordH G. All elements of finite groups have finite order. In general if.

An easy way to distinguish these particular types is by looking at orders of the elements. We prove that there is a bijective map from G C G a to Cl a. We will first show that each coset a H consists of m different elements.

The Order of an element of a group is the same as that of its inverse a-1. Suppose that p is the smallest prime dividing G. If G is a finite group or subgroup then the order of G is the number of elements of G.

The order of an element g in a group G is the smallest positive integer n such that gn e ng 0 in additive notation. Therefore 10 divides the order of G. The order of every element of a finite group is finite.

It is closed under multiplication and inversion. By the third Sylow theo-rem the number of such subgroups divides p and is congruent to 1 modulo q. Thus there are two groups of order n up to isomor-phism.

The number of cyclic subgroups of order p we should divide the number of elements of order pby the number of generators of a cyclic group of order p namely p p 1. The order of a subgroup H of group G divides the order of G. More precisely G H cdot textnumber of left cosets.

It helps to know that there are just 2 types of groups of order 4 the cyclic ones and the klein group type ones. This is a consequence of Cauchys theorem. However my book says that for finite G the image of G also has an order that divides the order of G.

Basic Properties of Orders Let Gbe a group written multiplicatively. Lagranges Theorem says that for any group G the order of any subgroup H of G divides the order of G or G H G. One can show that any subgroup of a free group is free.

If G is a finite group and H a subgroup of G then the order of H will divide the order of G. H This means that we can create a subgroup g or the cyclic group generated by an element g in G whose order will be the order of the element g since g e g 1 g 2 g n 1 where n is the order of the element g. If H is a subgroup of finite group G then the order of subgroup H divides the order of group G.

Feb 15 2012. Group homomorphism preserves identity inverses and subgroups. Definition Order of an Element.

The number of elements of a group ﬁnite or inﬁnite is called its order. H where G. Then is a homo-morphism since.

The fact that this. We denote the order of G by G. The order of a subgroup of a finite group divisor of the order of the group.

Let N be a normal subgroup of G such that the index G. This is easily seen to be a subgroup. Prove that H is in the center ZG.

Let us consider the coset decomposition of G relative to H. The First Proof of b. If ghas nite order suppose gn efor some n0.

So for finite group G its image also has to be finite. GGH GKby g gHgK. Homework Equations the Class Equation.

In general the order of any subgroup of G divides the order of G. So the total number of p-Sylow subgroups of S p is p 1p 1 p 2 which clearly divides p. If Hand Kare normal subgroups of a group Gand HK feg prove that Gis isomorphic to a subgroup of GH GK.

H is the index of H in G an integer. GHis onto then the order of Hdivides the order of G. Subgroup Containing All p-Sylow Subgroups of a Group Suppose that G is a finite group of order pan where p is a prime number and p does not divide n.

N is relatively prime to p. This shows that any group is isomorphic to a quotient of two free groups. To say ghas nite order in Gis equivalent to saying hgiis a nite group.

Homework Statement Let H be a normal subgroup of prime order p in a finite group G. Let H be any subgroup of order m of a finite group G of order n. This asserts the existence of -Sylow subgroups for every prime dividing the order of the group.

By the ﬁrst Sylow theorem G has a subgroup of order q. Let S be a set and letR be a subset ofFSThen S R FSH where H is the smallest normal subgroup of FS such that R HWesay then that. By part a the centralizer C G a is a subgroup of the finite group G.

Sylow theorems are in the next section so. The Lagrange theorem states. This is Lagranges theorem.

The only such number is 1 and hence there is a unique such subgroup. Hence the set of left cosets G C G a is a finite set and its order divides the order of G by Lagranges theorem. Elements have order 1222.

Each have the same number of members as the subgroup. Does the order of a subgroup divide the order of the group. For g2G the subgroup generated by gis hgi fgk.

Exponent of a finite group has precisely the same prime factors as order. Properties of the order of an element of the group. In particular Kerf is free.

As an immediate consequence of the above we see that the order of every element of a group divides the order of the group. Consider a general power of.